This a learning note from the class given by Yuanming Hu about Physical Simulation
Introduction
Two Views of Continuums
There are two basic methods for solving fluid equations
Lagrangian View: “What are my position and velocity?”
- Method based on particles
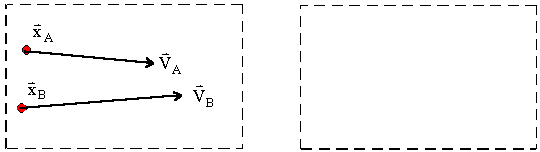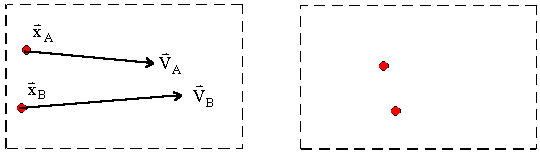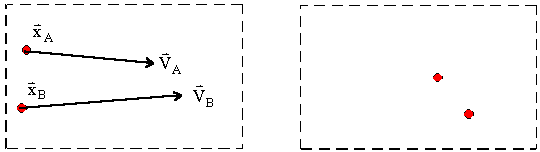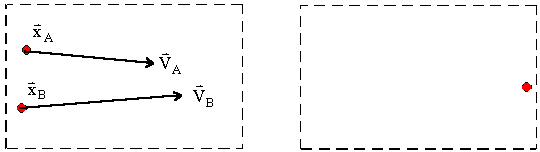
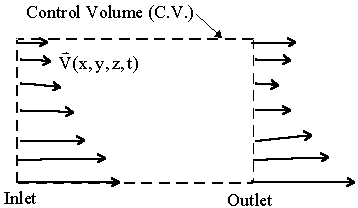
Eulerian View: “What is the material velocity passing by?”
- Method based on grid
Mass-Spring Systems
Mass Spring Systems are a physical simulation based on Lagrangian view, an object are seen as . Mass-spring systems are good for
Hooke’s Law
Newton’s second law of motion
Time integration
Time integration - Explicit
(1) Forward Euler (explicit)
(2) Semi implicit Euler (aka. symplectic Euler, explicit)
| Pros | Cons |
|---|---|
| Future depends only on past | Easy to explode |
| Easy to implement | Bad for stiff materials |
Explosion limit:
Time integration - Implicit
Backward Euler (often with Newton’s method, implicit)
Estimate $\textbf{x}_{t+1}$:
Linearize (one step of Newton’s method):
Clean up:
How to solve it
- Jacobi/Gauss-Seidel iterations (easy to implement)
- Conjugate gradients
Unify explicit and implicit integrators
- $\beta = 0$: forward/semi-implicit Euler (explicit)
- $\beta = 1/2$: middle-point (implicit)
- $\beta = 1$: backward Euler (implicit)
Solve faster
- Sparse matrices
- Conjugate gradients
- Preconditioning
Code
Based on Mass-Spring System, I wrote a simple rope simulator using OpenGL. I choose semi implicit time integration as it’s the most intuitive method without revolving other math libs dependency.
Source repo is here
