Real Time Collision Detection: Intro

A learning note while reading Real-Time Collision Detection by Christer Ericson

This is a personal blog so I’ll skip some of the common knowledge like general 3D math or linear algebra. This intro will list some of the key concepts used in collision detection that I haven’t heard of or find important enough to re-memorize again.

Polygons

A polygon is a closed figure with n sides, defined by an ordered set of three or more points in the plane in such a way that each point is connected to the next (and the last to the first) with a line segment.

Simple: A polygon is simple if no two nonconsecutive edges have a point in common. A simple polygon partitions the plane into two disjoint parts: the interior (the bounded area covered by the polygon) and the exterior (the unbounded area outside the polygon).
Convex/Concave vertex: A vertex is a convex vertex if the interior angle is less than or equal to 180 degrees. If the angle is larger than 180 degrees, it is instead called a concave (or reflex) vertex.
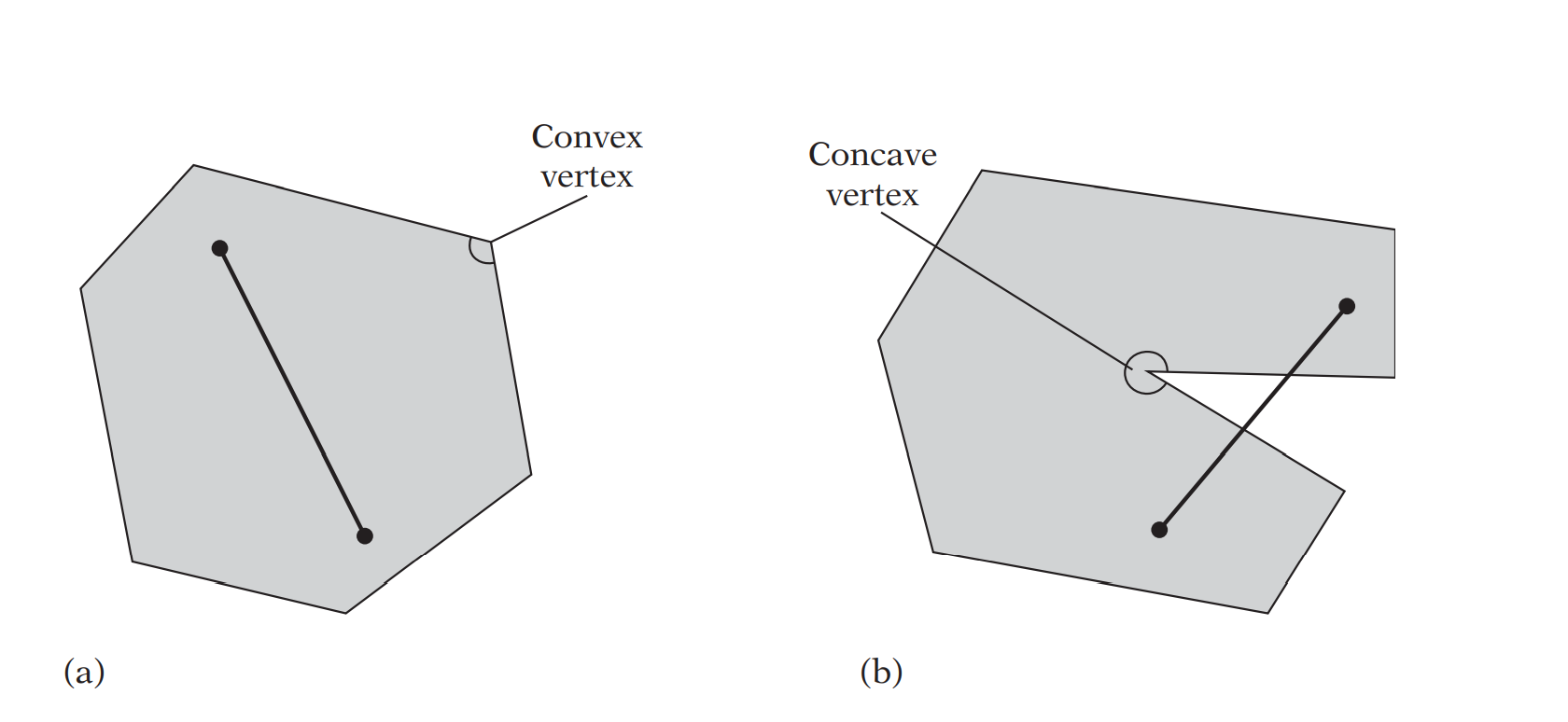
Convex/Concave polygon: A polygon P is a convex polygon if all line segments between any two points of P lie fully inside P. A polygon that is not convex is called a concave polygon. A polygon with one or more concave vertices is necessarily concave, but a polygon with only convex vertices is not always convex.
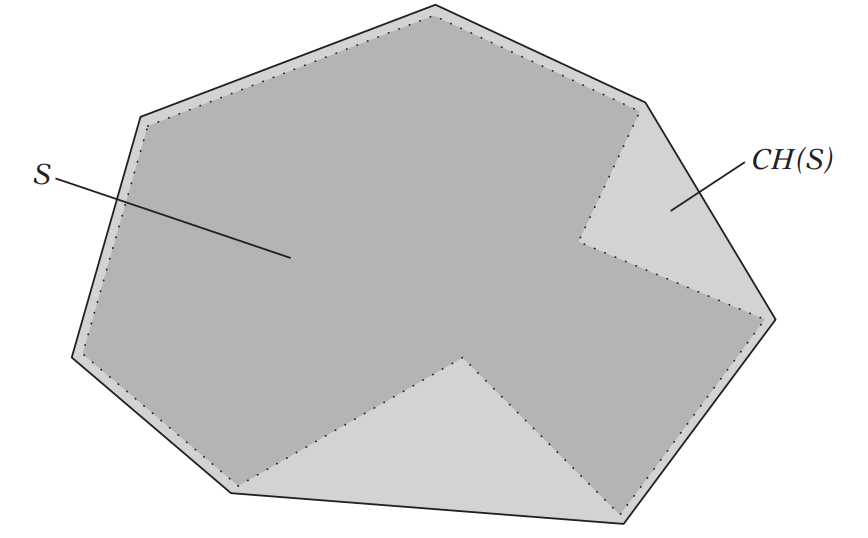
Convex hull: A convex point set $S$ is a set of points wherein the line segment between any two points in $S$ is also in $S$. Given a point set $S$, the convex hull of $S$, denoted $CH(S)$, is the smallest convex point set fully containing $S$. $CH(S)$ can also be described as the intersection of all convex point sets containing $S$.
Affine hull: Related to the convex hull is the affine hull, $AH(S)$. The affine hull is the lowest dimensional hyperplane that contains all points of $S$. That is, if $S$ contains just one point, $AH(S)$ is the point; if $S$ contains two points, $AH(S)$ is the line through them; if $S$ contains three noncollinear points, $AH(S)$ is the plane determined by them; and if $S$ contains four (or more) non co-planar points, $AH(S)$ is all of $\mathbb{R}^3$.

Test Polygon Convexity

Triangle

The triangle is the only n-sided polygon always guaranteed to be convex.

Quad

Frequently, quadrilaterals (or quads, for short) are the only primitives supported in addition to triangles.

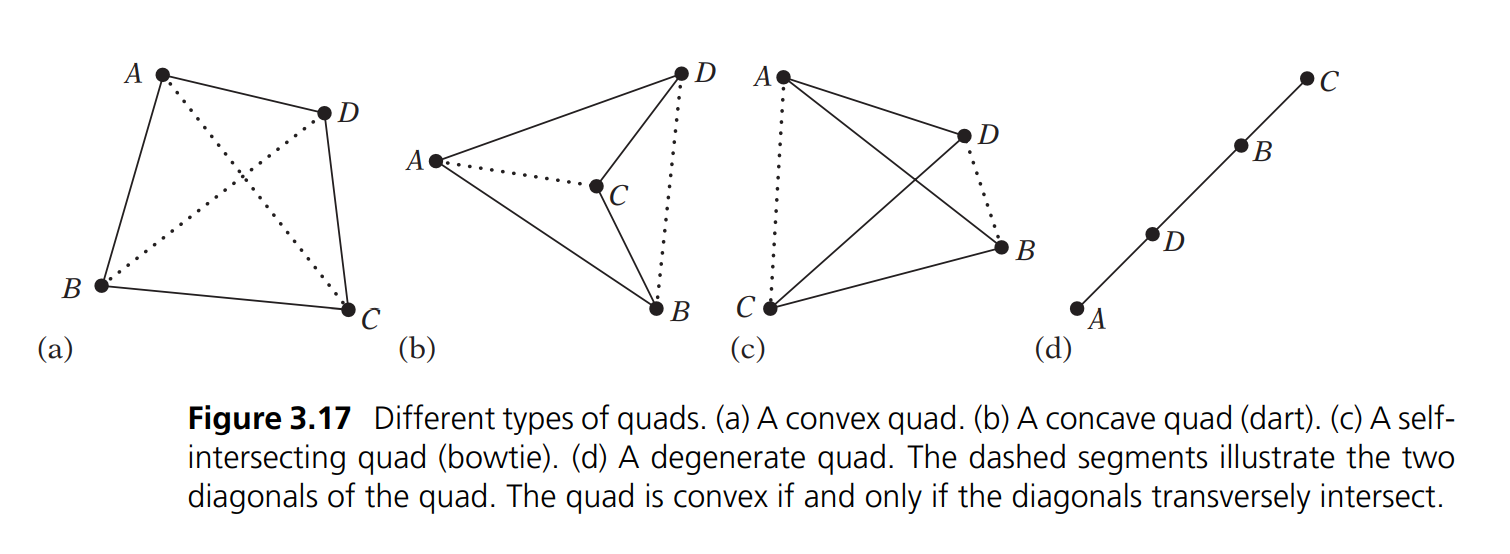
Different Type of Quads

The quad is therefore convex if

$(BC \times BA ) \cdot (BD \times BC) < 0\, \text{and} (AC \times AD ) \cdot (AC \times AB) < 0$

A straightforward implementation results in the following code:

// Test if quadrilateral (a, b, c, d) is convex
int IsConvexQuad(Point a, Point b, Point c, Point d)
{
	// Quad is nonconvex if Dot(Cross(bd, ba), Cross(bd, bc)) >= 0
	Vector bda = Cross(d - b, a - b);
	Vector bdc = Cross(d - b, c - b);
	if (Dot(bda, bdc) >= 0.0f) return 0;
	// Quad is now convex iff Dot(Cross(ac, ad), Cross(ac, ab)) < 0
	Vector acd = Cross(c - a, d - a);
	Vector acb = Cross(c - a, b - a);
	return Dot(acd, acb) < 0.0f;
}

General n-gons

For general $n$-gons, not just quads, a straightforward solution is to, for each polygon edge, test to see if all other vertices lie (strictly) on the same side of that edge. If the test is true for all edges, the polygon is convex, and otherwise it is concave. A separate check for coincident vertices is required to make the test robust. However, although easy to implement, this test is expensive for large polygons, with an $O(n^2)$ complexity in the number of vertices.

Polyhedra

Computing Convex Hulls

Among other uses, convex hulls can serve as tight bounding volumes for collision geometry.

Andrew’s Algorithm

One of the most robust and easy to implement 2D convex hull algorithms is Andrew’s algorithm.

The Quickhull Algorithm

Although Andrew’s algorithm works very well in 2D, it is not immediately clear how to extend it to work in 3D. An alternative method that works in both 2D and 3D is the Quickhull algorithm.

Voronoi Diagram

The Voronoi diagram is named after Georgy Voronoy, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation. Voronoi cells are also known as Thiessen polygons.

$R_{k}=\{x\in X\mid d(x,P_{k})\leq d(x,P_{j})\;{\text{for all}}\;j\neq k\}$

Minkowski Sum and Difference

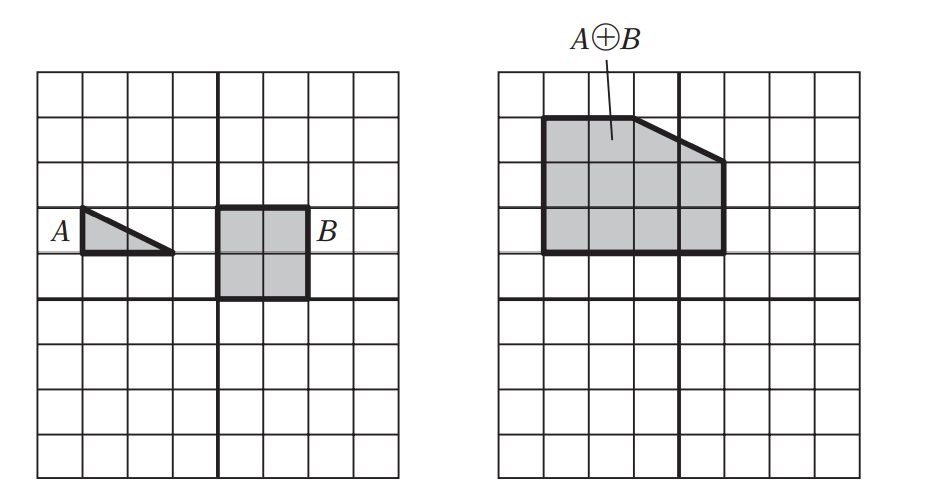
Minkowski Sum

Let $A$ and $B$ be two point sets, and let $\mathbf{a}$ and $\mathbf{b}$ be the position vectors corresponding to pairs of points in $A$ and $B$. The Minkowski sum, $A \oplus B$, is then defined as the set

$A \oplus B=\{\mathbf {a} + \mathbf {b} \,|\,\mathbf {a} \in A,\ \mathbf {b} \in B\}$

where $\mathbf {a} + \mathbf {b}$ is the vector sum of the position vectors $\mathbf{a}$ and $\mathbf{b}$.

Minkowski Sum Example

Minkowski Difference

The Minkowski difference of two point sets $A$ and $B$ is defined analogously to the Minkowski sum:

$\begin{equation} \begin{aligned} A \ominus B &= \{\mathbf {a} - \mathbf {b} \,|\,\mathbf {a} \in A,\ \mathbf {b} \in B\}\\ &= A \oplus (-B) \end{aligned} \end{equation}$

The Minkowski difference is important from a collision detection perspective because two point sets $A$ and $B$ collide (that is, have one or more points in common) if and only if their Minkowski difference $C (C = A \ominus B)$ contains the origin:

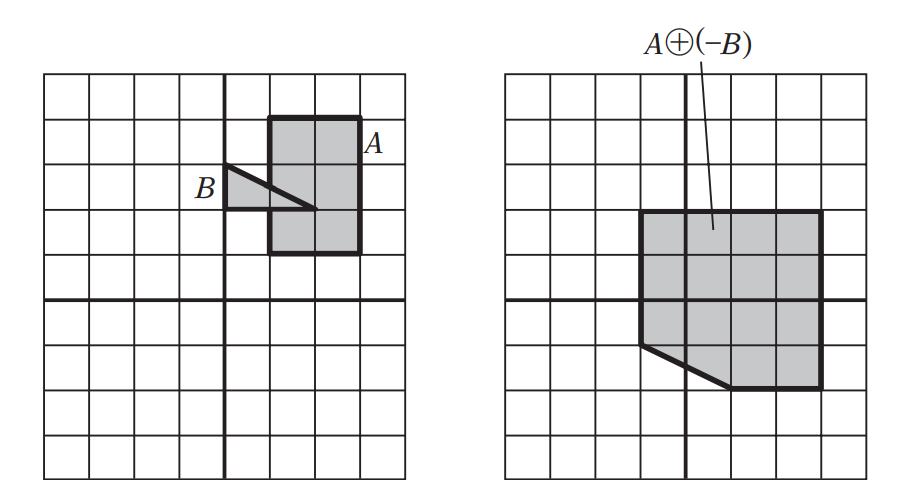
Minkowski Diff Example

In fact, it is possible to establish an even stronger result: computing the minimum distance between A and B is equivalent to computing the minimum distance between C and the origin. This fact is utilized in the GJK algorithm:

$\begin{equation} \begin{aligned} distance(A, B) &= min\left\{ \| \mathbf{a} - \mathbf{b} \| \,:\,\mathbf {a} \in A,\, \mathbf {b} \in B\ \right\}\\ &= min\left\{ \| \mathbf{c} \| \,:\,\mathbf {c} \in A \ominus B \right\} \end{aligned} \end{equation}$