Physical Simulation: Elasticity

Deformation

Deformation map $\phi : a$ (vector to vector) function that relates rest material position and deformed material position.

$\mathbf{x}_\mathbf{deformed} = \phi(\mathbf{x}_\mathbf{rest})$

Note: Deformation gradients are translational invariant

$\phi1 = \phi(\mathbf{x}\mathbf{rest})$ and $\phi2 = \phi(\mathbf{x}\mathbf{rest}) + \mathbf{c}$ have the same deformation gradients

Deformation gradient - $\textbf{F}$

$\textbf{F} \coloneqq \frac{\partial \textbf{x}_\textbf{deformed}}{\partial \textbf{x}_\textbf{rest}}$

Deform/rest volume ratio $J = det(\textbf{F})$

Hyperelasticity

Hyperelastic materials: materials whose stress-strain relationship is defined by a strain energy density function

$\Psi = \Psi(\textbf{F})$

Intuitive understanding: $\Psi$ is a potential function that penalizes deformation.

“Stress”: the material’s internal elastic forces
“Strain”: just replace it with deformation gradient F for now

Stress tensor

Stress stands for internal forces that infinitesimal material components exert on their neighborhood.

Based on our need, we use different measures of stress

The First Piola-Kirchhoff stress tensor (PK1): $\textbf{P}(\textbf{F}) = \frac{\partial \Psi(\textbf{F})}{\partial \textbf{F}}$ (easy to compute, but in rest space)
Kirchhoff stress: $\tau$
Cauchy stress tensor: $\sigma$ (symmetric, because of conservation of angular momentum)

Relationship: $\tau = J\sigma = \textbf{P}\textbf{F}^{T}$ $\textbf{P}=J\sigma\textbf{F}^{-T}$ Traction $\textbf{t} = \sigma^{T}\textbf{n}$

Intuition of $\textbf{P}=J\sigma\textbf{F}^{-T}$ :

$J$ compensate for material compression/expansion.
$\textbf{F}^{-T}$ compensates for material deformation. (Note that it’s $\textbf{F}^{-T}$ instead of $\textbf{F}^{-1}$ since we transform the normal n instead of x.)

Elastic moduli (isotropic materials)

Young’s modulus $E = \frac{\sigma}{\epsilon}$
Bulk modulus $K = -V \frac{dP}{dV}$
Poisson’s ratio $v \in [0.0, 0.5)$ (Auxetics have negative Poisson’s ratio)

Lamé parameters:

Lamé’s first parameter $\mu$
Lamé’s second parameter $\lambda$ (aka. shear modulus, denoted by $G$)

Useful conversion formula:

$K = \frac{E}{3(1-2v)} \\ \ \\ \lambda = \frac{Ev}{(1+v)(1-2v)} \\ \ \\ \mu = \frac{E}{2(1+v)}$

Hyperelastic material models

Popular ones in graphics

Linear elasticity (small deformation only)
Neo-Hookean
(Fixed) Corotated

See details at The Material Point Method for Simulating Continuum Materials

FEM(Finite Element Method) basics

The finite element method

Galerkin discretization scheme that builds discrete equations using weak formulations of continuous PDEs.

Wikipeida - https://en.wikipedia.org/wiki/Finite_element_method

Periodic Table of the Finite Elements - https://www-users.cse.umn.edu/~arnold/femtable/index.html

Linear tetrahedral (triangular) FEM

Linear tetrahedral finite elements (for elasticity) assume the deformation map $\phi$ is affine and thereby deformation gradient F is constant within a single tetrahedral element:

$\mathbf{x}_\mathbf{deformed} = \textbf{F}\mathbf{x}_\mathbf{rest} + \textbf{b}$

For every element $e$, its elastic potential energy

$U(e) = \int_{e} \Psi(\textbf{F(x)})\,\textbf{dx} = V_{e}\Psi(\textbf{F}_{e})$

Computing $\textbf{F}_{e}$ in linear tetrahedral finite elements

First let’s elimiate $\textbf{b}$

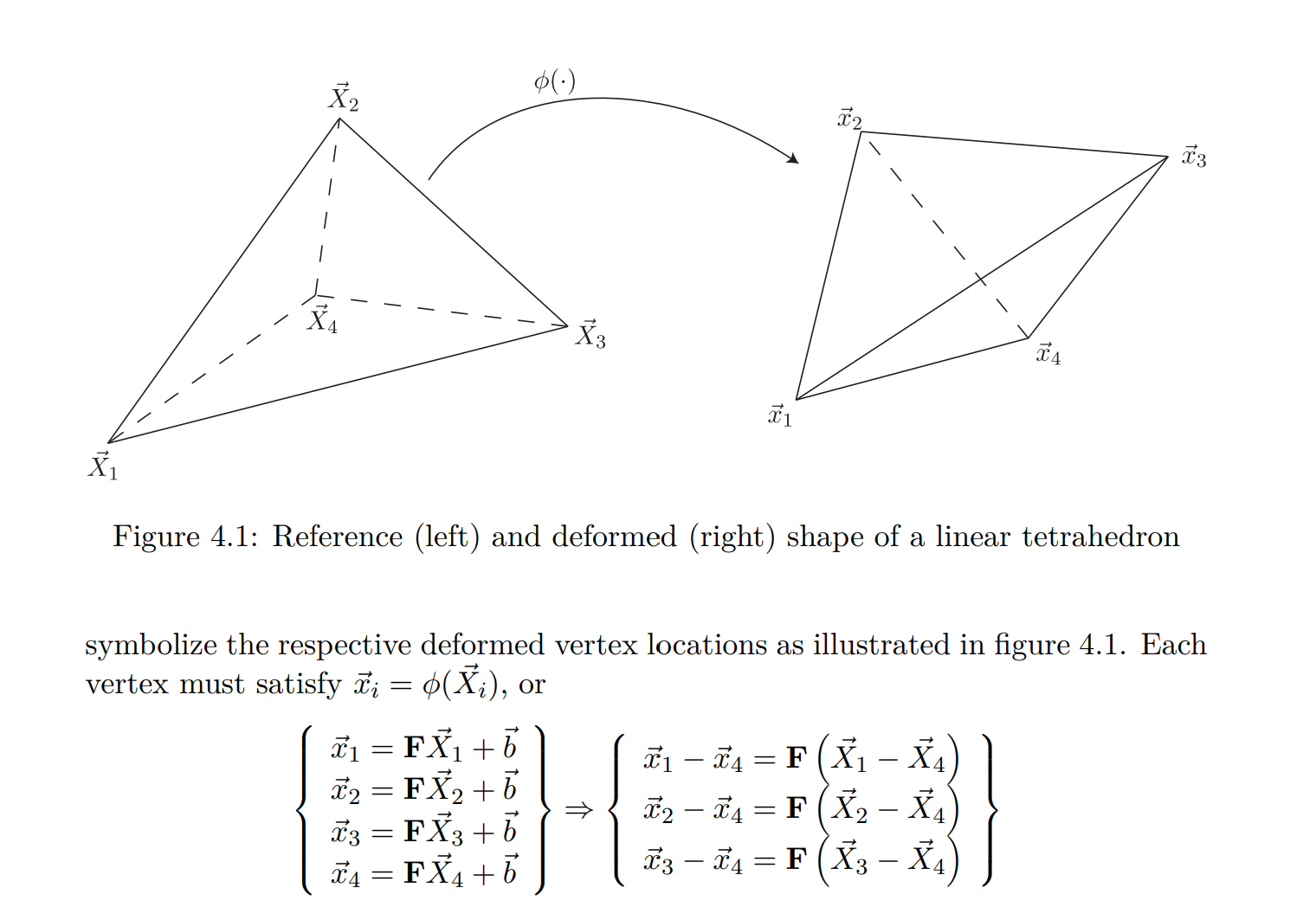
Linear FEM eliminate b

So now we have the equations

Linear FEM equations

Name $\textbf{B} = \textbf{D}_{m}^{-1}$, we have

$\textbf{F} = \textbf{D} \textbf{B}$

Note that $\textbf{B}$ is a constant throughout the physical process. Therefore it should be pre-computed.

Pseudo code

Linear FEM pseudo code

Extend reading

FEM Simulation of 3D Deformable Solids: A practitioner’s guide to theory, discretization and model reduction